It’s been very dry across much of Oklahoma this winter. In fact, according to the Oklahoma Mesonet, in the last 30 days, Norman, OK has only received 0.13″ of rain. Over the last 60 or even 90 days the situation isn’t much better. Thus, it wasn’t much of a surprise this evening when I looked out my office window at the National Weather Center and saw the following:
Contrary to what a few people initially thought, this is not a pretty sunset highlighting a low stratus cloud. This is actually the smoke from what I initially thought was an out-of-control grass fire in extreme eastern Moore, OK. (Turns out this was apparently a controlled burn, which is surprising given the relatively high fire danger and other wildfires burning in the vicinity.)
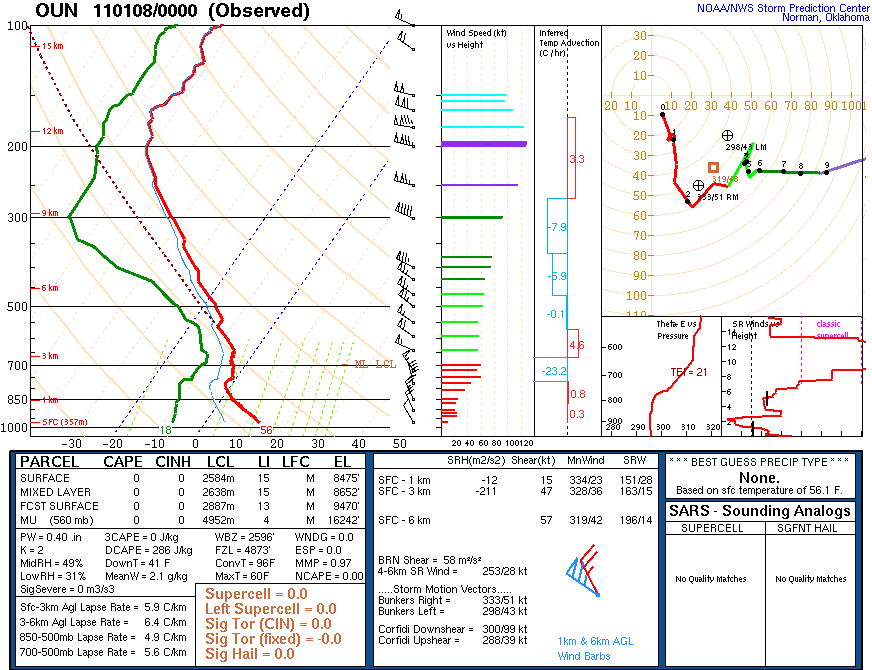
Have you ever wondered why oftentimes smoke plumes tend to look like this? Namely, it initially rises and then appears to flatter out along some constant altitude? Turns out the answer lies in the vertical temperature structure of the atmosphere and to illustrate it, we’ll take a look at an atmospheric sounding from Norman, OK (taken approximately the time of this photograph) displayed on a Skew-T/Log-P Diagram, or Skew-T for short.
Above (and below) are tonight’s 00 UTC 08 January 2011 (6 PM CST 07 January 2011)) for Norman, OK. Even though the sounding is dated 00 UTC, it was actually launched approximately 45-60 minutes prior to 00 UTC. In this sounding, notice that the temperature decreases rapidly with height from the surface to around 800-millibars. In fact, it cools at around 10C over the first kilometer above the ground. This cooling rate is known as the dry adiabatic lapse rate. This is the rate of cooling expected if we were to lift any parcel of dry air vertically. Through the concepts of buoyancy and convective instability, any parcel that is warmer than ambient air will accelerate upward on it’s own, any parcel that is cooler than the ambient air will accelerate downward on it’s own, and any parcel the same temperature as the ambient air will continue to do whatever it is doing.
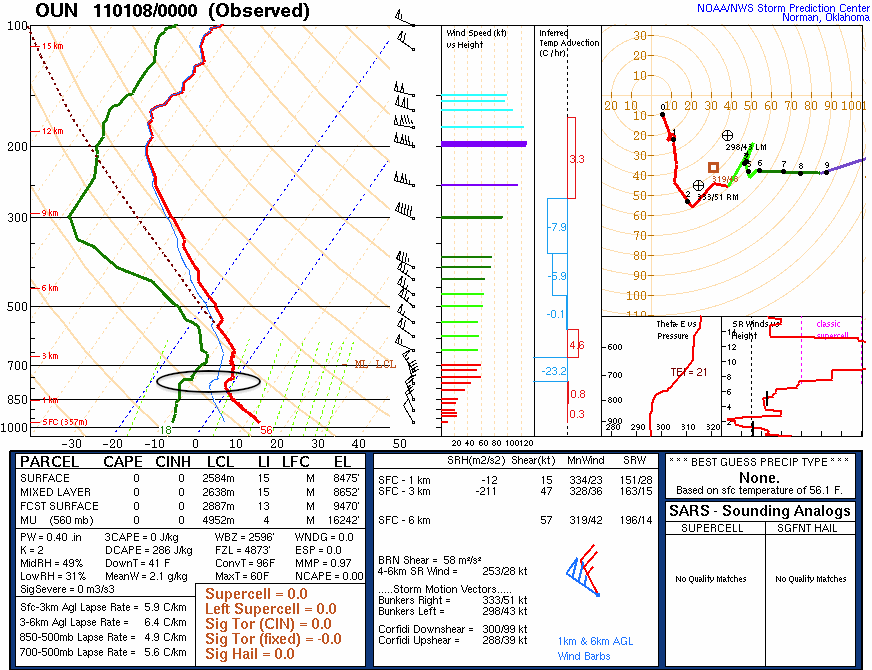
At around 800-millibars the temperature stops cooling as we increase height. In fact, it remains the same or even warms slightly! This warming with height is known as a temperature inversion, or inversion for short. I’ve circled this temperature inversion below.
So what does this have to do with the smoke plume? Well, the smoke from the fire acts like a parcel of dry air. This means that for every one kilometer above the ground, the temperature of the smoke would be expected to cool 10C. (In reality the temperature of the smoke would most likely cool at a slightly faster rate due to processes such as turbulent mixing.) If we were to assume that the temperature of the smoke was approximately the same temperature as the ambient temperature, or slightly warmer, we would expect the smoke to accelerate upward. However, as the smoke accelerates upward it begins to cool, as we previously mentioned. It continues to rise because it is approximately the same temperature as the air surrounding it, so it will remain doing what it had been doing (which was rising).
Eventually the smoke will reach the height of the temperature inversion and become colder than the air surrounding it. At this point the smoke will begin to descend until it reaches an altitude where it is in equilibrium with the ambient air temperature, typically at or slightly below the height of the temperature inversion. At this point the smoke will begin to spread out horizontally instead of vertically, frequently being blow in a specific direction by the wind, as was the case yesterday evening.
So, by seeing smoke plumes spread horizontally, instead of vertically, one is actually visualizing the altitude of a temperature inversions.